What is deep learning? opening the black box

• Forward propagation
  • A bad picture
  • A better picture
• Backward propagation
• Need to change the weights
• What is \(\nabla_\theta \L(\theta) \)
• What's the big deal

Somewhat based on https://campus.datacamp.com/courses/deep-learning-in-python

Forward propagation

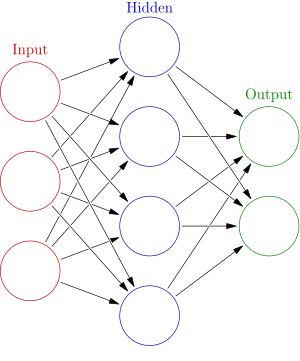
DL: better picture

DL: better picture

• All weights/parameters: \( \quad \theta = [W_1, b_1, W_2, b_2] \)
• The loss = scalar measure how bad $y(x, \theta)$ is.
  • For a single sample: \( \quad \ell(y(x, \theta), y_t) \)
  • For a dataset: \( \quad \mathcal{L}(\theta) = \sum_{x,y_t \in D} \ell(y(x, \theta), y_t) \)
• We need to change the weights \( \theta \)
  to improve loss \( \L(\theta) \).

• How to change weights \( \theta \) to improve loss \( \L(\theta) \)?
• Backprop: compute \( \nabla_\theta \mathcal{L}(\theta) = \left[ \frac{\partial \mathcal{L}}{\partial W_1}, \frac{\partial \mathcal{L}}{\partial b_1}, \frac{\partial \mathcal{L}}{\partial W_2}, \frac{\partial \mathcal{L}}{\partial b_2} \right] \)
• \( \nabla_\theta \mathcal{L}(\theta) \) = what happens to the loss if I wiggle \( \theta \)
• Backprop: the chain rule on an arbitrary graph

DL: What's the big deal?

• Stack more layers: deep learning...
• Universal function approximator
• Parametrization: build in prior knowledge
  • convolutional: locality and translation invariance
  • recurrent: sequential nature of data
• BUT
  • non-convex optimization: all bets are off
  • no bounds, no guarantees
  • hard to proof anything
• It works

Deep Learning: TLDR

Learn a hierarchy of features

The framework ecosystem

The framework ecosystem

• Old times
  • theano (U Montreal, Y Bengio group)
  • torch (NYU, Yann LeCun group)
  • MATLAB (U Toronto, Geoff Hinton ;)
• Now
  • tensorflow (Google, conceptually close to theano)
    • keras will become new standard
  • pytorch (FAIR, directly descending from torch)
  • ONNX <- one standard to rule them all
    • caffe2, chainer, mxnet, etc.

theano / tensorflow design

• First define the graph
• Then run it multiple times (Session)
• tf: Too low-level for most users
• Many divergent high level libraries on top
  • tf.slim, tf.keras, sonnet, tf.layers, ...
• Recently Keras was adopted as standard
  • Torch-like design

pytorch design

• Construct the computational graph on the go
  (while doing the forward pass)
• "define by run"
• Reduces boilerplate code *a lot*
• Flexibility: forward pass can be different every iteration (depending on input)
• tf tries to imitate this model with "eager mode"

my advice for learning DL

Just Do It

“ What I cannot create,
I do not understand ”

Richard Feyman

actual advice

• Work in two stages
  1. Fast iteration (playground) → notebooks
  2. Condense it → version controlled python scripts
• 1. Fast iteration stage:
  • take everything apart
  • no structure, no abstractions
• 2. Condense it
  • carefully think about the right abstractions
  • Use frameworks (e.g. pytorch-lightning, ...)
• github repo's can be a great starting point
  • ..but start from scratch a couple times

DL: math

• ML = optimization
• Gradient descent
• SGD = Stochastic gradient descent
• Backpropagation revisited
• Beyond SGD

ML = optimization

This is all of ML:

Gradient descent

Find argmin by taking little steps $\alpha$ along :

$$\theta \gets \theta - \alpha \nabla_\theta \L(\theta)$$

Stochastic Gradient descent

Oops \(\nabla_\theta \L(\theta)\) is expensive, sums over all data.

Ok instead of \(\L (\theta) = \sum_{x,y \in D} \ell(x,y; \theta) \)

Let us use \(\L^{mb} (\theta) = \sum_{x,y \in mb} \ell(x,y; \theta) \)

\(\L^{mb} (\theta) \) is the loss for one minibatch.

Backpropagation

Compute \( \nabla_\theta \L^{mb} (\theta) \) by chain rule:

reverse the computation graph.

Beyond SGD

• SGD is the simplest thing you can do.
  What else is out there?
• Second order optimization.. meh
• Adaptive learning rate methods