Deep Learning.
Guest lecture / 2018-12-03
Intro to Data Science, Fall 2018 @ CCNY
Tom Sercu - homepage - twitter - github.
This guest lecture - Preface - Main slides - Figure - lab (github)
Recapping part 1 (pdf)
DL: Successes
Object recognition
Speech recognition
Machine Translation
"simple" Input->Output ML problems!
DL: Frontiers
Common sense
What is deep learning? opening the black box
- Forward propagation
- A bad picture
- A better picture
- Backward propagation
- Need to change the weights
- What is \(\nabla_\theta \L(\theta) \)
- What's the big deal
Somewhat based on https://campus.datacamp.com/courses/deep-learning-in-python
Forward propagation
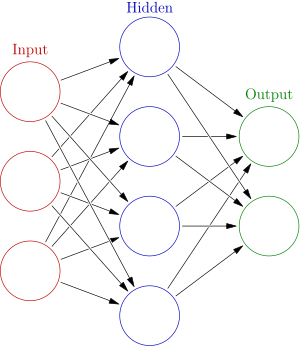
DL: better picture
FigureDL: better picture
- All weights/parameters: \( \quad \theta = [W_1, b_1, W_2, b_2] \)
- The loss = scalar measure how bad $y(x)$ is.
- For a single sample: \( \quad \ell(y(x), y_t; \theta) \)
- For a dataset: \( \quad \mathcal{L}(\theta) = \sum_{x,y \in D} \ell(y(x), y_t; \theta) \)
- We need to change the weights \( \theta \)
to improve loss \( \L(\theta) \).
- How to change weights \( \theta \) to improve loss \( \L(\theta) \)?
- Backprop: compute \( \nabla_\theta \mathcal{L}(\theta) = \left[ \frac{\partial \mathcal{L}}{\partial W_1}, \frac{\partial \mathcal{L}}{\partial b_1}, \frac{\partial \mathcal{L}}{\partial W_2}, \frac{\partial \mathcal{L}}{\partial b_2} \right] \)
- \( \nabla_\theta \mathcal{L}(\theta) \) = what happens to the loss if I wiggle \( \theta \)
- Backprop: the chain rule on an arbitrary graph
DL: What's the big deal?
- Stack more layers: deep learning...
- Universal function approximator
- Parametrization: build in prior knowledge
- convolutional: locality and translation invariance
- recurrent: sequential nature of data
- BUT
- non-convex optimization: all bets are off
- no bounds, no guarantees
- hard to proof anything
- It works
Deep Learning: TLDR
Learn a hierarchy of features
The framework ecosystem





The framework ecosystem
- Old times
- theano (U Montreal, Y Bengio group)
- torch (NYU, Yann LeCun group)
- MATLAB (U Toronto, Geoff Hinton ;)
- Now
- tensorflow (Google, conceptually close to theano)
- keras will become new standard
- pytorch (FAIR, directly descending from torch)
- ONNX <- one standard to rule them all
- caffe2, chainer, mxnet, etc.
- tensorflow (Google, conceptually close to theano)
theano / tensorflow design
- First define the graph
- Then run it multiple times (Session)
- tf: Too low-level for most users
- Many divergent high level libraries on top
- tf.slim, tf.keras, sonnet, tf.layers, ...
- Recently Keras was adopted as standard
- Torch-like design
pytorch design
- Construct the computational graph on the go
(while doing the forward pass) - "define by run"
- Reduces boilerplate code *a lot*
- Flexibility: forward pass can be different every iteration (depending on input)
- tf tries to imitate this model with "eager mode"
I've been using PyTorch a few months now and I've never felt better. I have more energy. My skin is clearer. My eye sight has improved.
— Andrej Karpathy (@karpathy) May 26, 2017
my advice for learning DL
Just Do It
“ What I cannot create,
I do not understand ”
Richard Feyman
actual advice
- Work in two stages
- Fast iteration (playground) -> notebooks
- Condense it -> version controlled python scripts
- 1. Fast iteration stage:
- take everything apart
- no structure, no abstractions
- 2. Condense it
- carefully think about the right abstractions
- github repo's can be a great starting point
- ..but start from scratch a couple times
DL: math
- ML = optimization
- Gradient descent
- SGD = Stochastic gradient descent
- Backpropagation revisited
- Beyond SGD
ML = optimization
This is all of ML:
$$\arg\min_\theta \L(\theta)$$Gradient descent
Find argmin by taking little steps $\alpha$ along :
$$\nabla_\theta \L(\theta)$$$$\theta \gets \theta - \alpha \nabla_\theta \L(\theta)$$
Stochastic Gradient descent
Oops \(\nabla_\theta \L(\theta)\) is expensive, sums over all data.
Ok instead of \(\L (\theta) = \sum_{x,y \in D} \ell(x,y; \theta) \)
Let us use \(\L^{mb} (\theta) = \sum_{x,y \in mb} \ell(x,y; \theta) \)
\(\L^{mb} (\theta) \) is the loss for one minibatch.
Backpropagation
Compute \( \nabla_\theta \L^{mb} (\theta) \) by chain rule:
reverse the computation graph.
Beyond SGD
- SGD is the simplest thing you can do.
What else is out there? - Second order optimization.. meh
- Adaptive learning rate methods